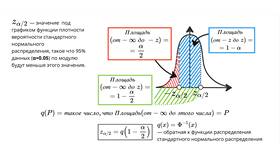
Доверительные интервалы представляют диапазон значений, который с определенной вероятностью содержит истинный параметр генеральной совокупности. Они широко используются в статистике для оценки точности измерений и результатов исследований.
Содержание
Основные понятия доверительных интервалов
- Доверительный уровень (обычно 90%, 95% или 99%)
- Точечная оценка параметра
- Стандартная ошибка
- Критическое значение распределения
Формула доверительного интервала для среднего
Для нормально распределенной совокупности при известном σ:
| ДИ = | X̄ ± Zα/2 × (σ/√n) |
| Где: | X̄ - выборочное среднее, Z - критическое значение, σ - стандартное отклонение, n - объем выборки |
Пошаговый алгоритм построения
Определение параметров
- Выберите доверительный уровень (1-α)
- Рассчитайте выборочную статистику (среднее, пропорцию)
- Определите стандартную ошибку оценки
Выбор соответствующего распределения
| Условия | Используемое распределение |
| Известно σ, n > 30 | Нормальное (Z-распределение) |
| Неизвестно σ, n < 30 | t-распределение Стьюдента |
| Доли и пропорции | Нормальное приближение |
Пример расчета для среднего
При следующих условиях:
- Выборочное среднее (X̄) = 50
- Стандартное отклонение (σ) = 10
- Объем выборки (n) = 100
- Доверительный уровень = 95%
Расчет интервала
- Найдите критическое значение Z для 95% (1.96)
- Рассчитайте стандартную ошибку: σ/√n = 10/10 = 1
- Вычислите предельную ошибку: 1.96 × 1 = 1.96
- Постройте интервал: 50 ± 1.96 → [48.04, 51.96]
Особые случаи
Доверительный интервал для пропорции
Формула:
| ДИp = | p̂ ± Zα/2 × √(p̂(1-p̂)/n |
| Где: | p̂ - выборочная пропорция |
Практические рекомендации
- Для малых выборок используйте поправки (например, Уилсона)
- При работе с t-распределением учитывайте степени свободы
- Проверяйте условия применимости формул
- Используйте статистические пакеты для сложных случаев