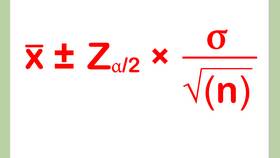Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим методику расчета стандартного доверительного интервала для среднего значения при известном стандартном отклонении.
Содержание
Основные понятия
| Термин | Обозначение | Описание |
| Выборочное среднее | x̄ | Среднее значение выборки |
| Стандартное отклонение | σ | Мера разброса данных |
| Объем выборки | n | Количество наблюдений |
| Уровень доверия | 1-α | Вероятность покрытия параметра |
Формула доверительного интервала
Доверительный интервал для среднего при известном σ вычисляется по формуле:
CI = x̄ ± zα/2 × (σ/√n)
- CI - доверительный интервал
- zα/2 - критическое значение z-распределения
- σ/√n - стандартная ошибка среднего
Пошаговый алгоритм расчета
Определение параметров выборки
- Вычислите выборочное среднее x̄
- Определите известное стандартное отклонение σ
- Зафиксируйте объем выборки n
- Выберите уровень доверия (обычно 95%)
Нахождение критического значения
| Уровень доверия | zα/2 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
Вычисление стандартной ошибки
SE = σ/√n
- SE - стандартная ошибка среднего
- σ - стандартное отклонение генеральной совокупности
- n - объем выборки
Расчет границ интервала
- Нижняя граница: x̄ - zα/2×SE
- Верхняя граница: x̄ + zα/2×SE
Пример расчета
| Параметр | Значение |
| Выборочное среднее (x̄) | 50 |
| Стандартное отклонение (σ) | 10 |
| Объем выборки (n) | 100 |
| Уровень доверия | 95% |
| Доверительный интервал | 50 ± 1.96 × (10/√100) = [48.04, 51.96] |
Условия применения
- Нормальное распределение генеральной совокупности
- Известное стандартное отклонение σ
- Объем выборки n ≥ 30 (для центральной предельной теоремы)
- Случайная и независимая выборка
Интерпретация результатов
Доверительный интервал [48.04, 51.96] означает, что с вероятностью 95% истинное среднее значение генеральной совокупности находится в этом диапазоне.